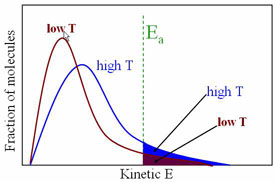
Effect of Temperature on rate of Reaction
The rate of reaction is a function of many things, including surface area, concentration and temperature. For a reaction to take place, the molecuels must collide with enough energy (called the Activation Energy, EA) Consider the reactant molecules to be at a particular temperature. By definition, the molecules have an average kinetic energy, some with more than the average, some with less. If we increase the temperature of a system, the average kinetic energy will increase and the number of molecules with the 'minimum' energy to react, thus increasing the frequency (rate) of reaction.

Svante Arrhenius has shown that for simple reactions, the equation
k
= Ae-Ea/RT →
ln k = -EA/RT
+
ln A
where k = rate constant, A is the collision frequency factor (function of the nature of reaction) R is the gas constant, T is the absolute temperature, EA is the activation energy, and e is the base of the natural logarithms. We want to know the relationship between rate of reactions and two different temperatures. After some creative algebra, we can transform the Arrehenius equation into something managable:
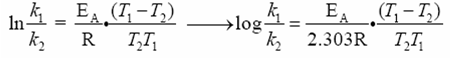
k is the rate constant at temperature
T, and k' is the rate
at T'.
In this
experiment, the reaction to be studied is the oxidation of HI to I2
by the action of H2O2
according to the equation
1
H2O2
+ 2 HI → 2 H2O + 1 I2
This reaction has been shown to be a second order reaction, first with respect to [HI], first with respect to [H2O2]. The experimentally determined rate law is of the form:
rate
= k[HI][H2O2]
The total volume of the solution containing the components of the reaction is kept constant during the course of this experiment; as another simplification, conditions are adjusted so that the reaction follows pseudo first order kinetics. This is done by maintaining the concentration of [HI], so the rate law becomes
rate
= k'[H2O2] where k' = k[HI]
This reaction will thus behave is a pseudo first order kinetics under these conditions.
To calculate the activation energy Ea, we simply need to determine the ratio of the rate constants k1/k2 at two different temperatures T2 and T1. There exists many different ways of determining rate constants. Here, we will measure the time taken to produce identical amounts of I2 at two temperatures, T and T'. We will have a series of data that is amount of Na2S2O3 and time. If we graph this (amount of Na2S2O3 (x) vs. time(y) using a computer and getting the equation and R2) the slope will be how much time is required per mole of Na2S2O3. Since time and rate are inversely proportional we can obtain the rate constant ratios by:
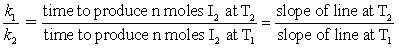
One experiment will be performed at temperature T2, and another at different temperature T1, using the same volumes and concentrations of reactants in both experiments. The time required to produce the same amount of I2 at each of the two temperatures will be measured and used to calculate k1/k2.
In this experiment, HI is produced by dissolving KI in a solution containing an excess of H2SO4:
1
H2SO4
+ 1 KI → 1 HI + KHSO4
Starch is added to this solution as the indicator of free iodine. We start the stopwatch at the moment we add our second reactant, H2O2. Of course the production of I2 begins immediately, and the blue color will instantly appear. A measured volume of 0.1 M Na2S2O3 is then added, causing the blue color to disappear due to the reduction of the I2 by thiosulfate. The solution will stay colorless until enough additional I2 is produced by H2O2-HI oxidation to react with the remaining Na2S2O3 in the solution. At this point the blue color will reappear. The time is noted. This represents the time required to produce I2 equivalent to the Na2S2O3 in the volume of 0.1 M Na2S2O3 which was added.
The entire reaction will be repeated with the same concentrations, but at a different temperature.
11 min screencast of the 'concept' of the lab
Chemicals needed- KI, 0.100 M Na2S2O3, 3% H2O2, starch solution, 6M H2SO4, ice
2. Place a 400 mL beaker on the lab balance, and add 1.00 g
of KI to it. It is important to get as close to 1.00 g as possible as
you want
the masses to be the same for both runs.
3. Dissolve the KI in about 250 mL of water. Add 15 mL of 6M
H2SO4 (caution!) and
carefully place the beaker in the
1000 mL water (ice?) bath. Place a stir bar in the solution and place
the
entire system on a stir plate and turn it on (no heat!!)
4. Make 50 mL of a 0.6% H2O2
solution
(10 mL 3% H2O2 and 40 mL
DI H2O) exact volumes
are best.
5. Carefully measure out 5.0 mL of this solution and place
it in a test tube, which is sitting in the 250 mL water bath beaker.
Put a
stopper on the test tube.
6. Rinse your buret twice and then fill it with 0.100 M Na2S2O3.
7. You want to wait until everything is at the desired
temperature before you go any further. Once you start the reaction, you
will
want to keep the system stirring to keep everything at the same (water
bath)
temperature.
8. Position the 400 mL beaker (plus its water bath) under
the buret. Record the temperature of the solution.
9. Add 4-6 drops of starch indicator to the 400 mL beaker.
10. Add the H2O2 to the
solution and
begin timing. The solution should immediately turn blue.
That’s a good thing.
The stopwatch does not get stopped until you have your (~12-20)
measurements.
11. One student should be reading the buret and recording
data (known as buret person), whilst the other watch the clock and the
solution
for the color change (clock person)
12. Buret person measures the volume in the buret. Then they
add about 1 mL of solution and write down the new volume (how much was
just
added?) The solution should turn clear. At the instant the solution
turns blue
again, (clock person calls out the time, since they are watching the
reaction)
record the time (buret person).
13. Buret person adds 1 more mL, measures and records the
new volume. The solution turns clear. When it turns blue again, measure
and
record the time.
14. Continue this procedure until you have added more than
20 mL of Na2S2O3
or until the blue color just
stops coming back.